Introduction
In order to model the optimal heat transfer in the condensing end of the heat pipe, the heat transfer coefficient for the convection across the heatsink needed to be determined. In order to accomplish this, research was done on convective heat transfer in order to find an approximation for the value. This approximation was then tested experimentally to determine its accuracy.The heatsink was modeled as having two distinct parts, the cylindrical base and the planar fins. The base can be modeled simply as an aluminum pipe. The fins will be approximated as vertical planes. Since each fin is small and aluminum has a high thermal conductivity, it will be assumed that the entire fin is at a single temperature.
Measurements
The following measurements were found using a micrometer and 0.01g digital scale.
Mass: 10.80 g
Surface Area: 1.131*10-2 m2
Fin Length: 0.99 cm
Fin Width: 1.00 cm
Fin Thickness: 0.635 mm
Inner Base Diameter: 2.89 cm
Outer Base Diameter: 2.99 cm
Fin Length: 0.99 cm
Fin Width: 1.00 cm
Fin Thickness: 0.635 mm
Inner Base Diameter: 2.89 cm
Outer Base Diameter: 2.99 cm
Theoretical Approximation
Since the equation for the heat transfer coefficient varies depending on the magnitude of the heatsink's Rayleigh number, the Rayleigh number was first calculated using the equation below.
g = acceleration due to gravity
β = inverse of absolute temperature
Ts = temperature of heatsink (assumed 50˚C)
T∞ = ambient temperature (assumed 23.5˚C)
L = length of heatsink fin
cp = specific heat of fluid (air)
μ = dynamic viscosity of fluid (air)
k = thermal conductivity of fluid (air)
v = kinematic viscosity of fluid (air)
Upon plugging in the values, the Rayleigh number was found to be 2.69*103. According to Wikipedia, the equation for the heat transfer coefficient (h) was then as follows:
where τ is a time constant defined by [6]
∆T = the temperature difference between the heatsink and the ambient air
m = mass of heatsink
c = specific heat of aluminum
A = surface area of heatsink
By plotting the data measured and finding a regression curve to fit the model above, h can be experimentally determined. Below is a plot of the data and the best fit curve. Note that the temperatures are plotted, not the temperature difference as the ambient temperature was not exactly known.
T∞ = ambient temperature (assumed 23.5˚C)
L = length of heatsink fin
cp = specific heat of fluid (air)
μ = dynamic viscosity of fluid (air)
k = thermal conductivity of fluid (air)
v = kinematic viscosity of fluid (air)
Upon plugging in the values, the Rayleigh number was found to be 2.69*103. According to Wikipedia, the equation for the heat transfer coefficient (h) was then as follows:
Pr is the Prandtl number which is found using the equation below and equals 0.69 [5].
Putting all the values together, the heat transfer coefficient for each heatsink fin was calculated to be 11.26 W/m2-k.
Experimental Determination
Procedure
A stand was made using a small rectangle of foam board with three paperclips punctured through the foam. The paperclips were unfolded and oriented vertically. The paperclips were arranged on the foam in an equilateral triangle spaced so that the heatsink could rest upon the paperclips. The stand served to allow even airflow across the heatsink and to minimize heat transfer via conduction since the contacts with the stand were very small. The figure below shows the stand that was made.
 |
| Heatsink resting on testing apparatus |
Thermal compound was spread around the interior of the heatsink in an attempt to match the conditions of the heat pipe and to increase the emissivity of the heatsink's surface. The heatsink was then heated on a hot stove for two minutes. Once sufficiently hot, the heatsink was transferred to the stand.
In ten second intervals, the temperature of the heatsink was found using an infrared thermometer pointed at the thermal compound on the inside of the heatsink. Due to the lack of directional accuracy when pointing the thermometer, the temperature was taken in small sweeping movements across the heatsink and the maximum value measured was recorded. 51 measurements were taken.
Data and Calculations
The change in temperature over time of the heat sink should follow the equation
where τ is a time constant defined by [6]
m = mass of heatsink
c = specific heat of aluminum
A = surface area of heatsink
By plotting the data measured and finding a regression curve to fit the model above, h can be experimentally determined. Below is a plot of the data and the best fit curve. Note that the temperatures are plotted, not the temperature difference as the ambient temperature was not exactly known.
The time constant associated with the best fit curve is 102.25. This can then be converted to the heat transfer coefficient.
The experiment was run a second time in order to confirm the results. The time constant in this second run was 110.49. The data from the second run is shown below
The experimental heat transfer coefficient was found to be approximately 8.3616 W/(m2-K) after two runs.
Conclusion
The experimental result is 25.7% off from the theoretical value. This could be due to a number of factors. First, the low emissivity of the aluminum made taking measurements difficult as infrared thermometers have trouble reading the low IR emissions from aluminum. Additionally, the thermometer used was not very precise and only rated to be within a few degrees of the actual temperature of the heatsink.
Additionally, the theoretical calculation is meant only for the heat transfer of the fins while the experimental calculation accounts for the entire heatsink, including the interior which would have a different heat transfer coefficient than the fins, especially with the thermal compound that was added to the inside.
Additionally, the theoretical calculation is meant only for the heat transfer of the fins while the experimental calculation accounts for the entire heatsink, including the interior which would have a different heat transfer coefficient than the fins, especially with the thermal compound that was added to the inside.
Finally, the lack of sufficient airflow across the heatsink may have caused a disparity between the temperature of the air in the room and the air around the heatsink. Without good airflow, the air surrounding the heatsink would heat up higher than the ambient temperature of the room thereby decreasing the temperature difference between the fins and ambient and slowing heat transfer. As showed in the data collected, the temperature seemed to level off around 28˚C indicating that the ambient temperature of the air around the heatsink was not the 23.5˚C of the rest of the room.

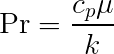




No comments:
Post a Comment